恩格玛机

恩格玛机（Enigma）

介绍

恩尼格玛密码机（德语：Enigma，又译恩尼格密码机、哑谜机、奇谜机或谜式密码机）是一种用于加密与解密文件的密码机。确切地说，恩尼格玛是对二战时期纳粹德国使用的一系列相似的转子机械加解密机器的统称，它包括了许多不同的型号，为密码学对称加密算法的流加密。

20世纪20年代早期，恩尼格玛密码机开始应用于商业，一些国家的军队与政府也使用过该密码机，密码机的主要用户包括第二次世界大战时的纳粹德国。

在恩尼格玛密码机的所有版本中，最著名的是德国使用的军用版本。尽管此机器的安全性较高，但盟军的密码学家们还是成功地破译了大量由这种机器加密的信息。1932年，波兰密码学家马里安·雷耶夫斯基、杰尔兹·罗佐基和亨里克·佐加尔斯基根据恩尼格玛机的原理破译了它。早在1939年中期，波兰政府就将此破译方法告知了英国和法国，但直到1941年英国海军捕获德国U-110潜艇，从中得到密码机和密码本后才成功破译。对于恩尼格玛的破译使得纳粹海军对英美商船补给船的大量攻击失效。盟军的情报部门将破译出来的密码称为ULTRA，ULTRA极大地帮助了西欧的盟军部队。关于ULTRA到底对战争有多大贡献尚存争论，但普遍认为盟军在西欧的胜利能够提前两年，完全是恩尼格玛密码机被成功破译的缘故。

尽管恩尼格玛密码机在加密方面有不足之处，但是经其加密的文件依然很难破译。盟军能够破译恩尼格玛是因为德国军队犯了一些大的错误，如没有像海军一样每月更新密码、使用步骤错误、机器或密码本被缴获等等，但这在1944年后英国开发出原始电脑后，即使每月更新也无济于事。

Enigma-Machine原理

凯撒密码（Caesar cipher）

罗马共和时期凯撒大帝曾发明一种文本加密方法，利用字母表的替换来对字母进行加密。交流者预先规定一个字母偏移量，根据字母偏移量将26个英文字母向后移动形成一张映射表，明文中的所有字母逐个对应字母表中的偏移字母产生暗文。

caesar cipher

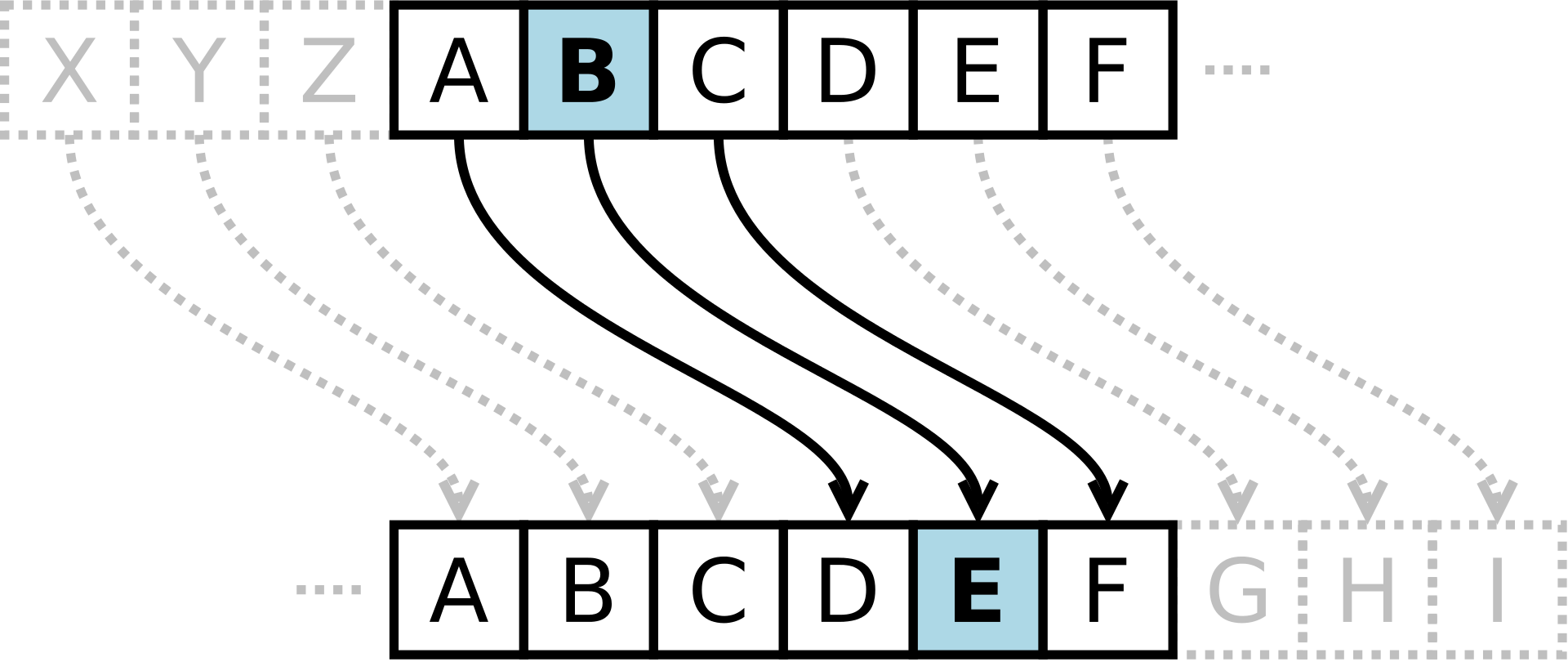
上图为一个偏移量为3的凯撒密码字母表，所有的字母A将被替换成D，B变成E，以此类推，从而形成一种替换加密的效果。
一个n移位的凯撒密码编码过程可以理解为

$E_n(X)=(X+n)\%26$

解码过程则是

$D_n(X)=(X-n)\%26$

转子（Rotor）

凯撒密码需要一个特定偏移量来制定一张密码表，然后人为的依照密码表进行字母的映射操作，可否使用一个建议的装置来实现这样一个映射操作呢？
很显然需要一个可以循环转动的表盘，这就是恩格玛机中的零件——转子。

转子

每一个转子相当于一张密码表，其表盘上分别是26个英文字母的触点，另一端连接着输入信号，当输入字母x时，经过转子会输出为y字母，从而完成映射。
转子转动的位置就可以代表偏移量，26个转动状态分别代表26个偏移量的偏移，也就是说一个转子可以实现26张密码字母表，这为恩格玛机复杂的编码过程提供了基础。
转子的编码具有“自反性”，即输入为x，输出为y时，当输入为y时，输出也是x。这为解码过程提供了相当大的便利。

多转子(Multiple Rotors)

一个转子的编解码至多只需要测试26张密码表就可以获得正确的结果，这显然是不能够作为密码传输的编码方式的，破解方只需要叫来26个人每个人按照一个偏移量（0~25）解码密文就一定可以有一份正确的明文。
解决这个问题的办法是增加转子的数量，即级联多个转子来进行编码，从一个转子输出的字母y不直接输出而是进入到下一个转子进行编码得到字母z。

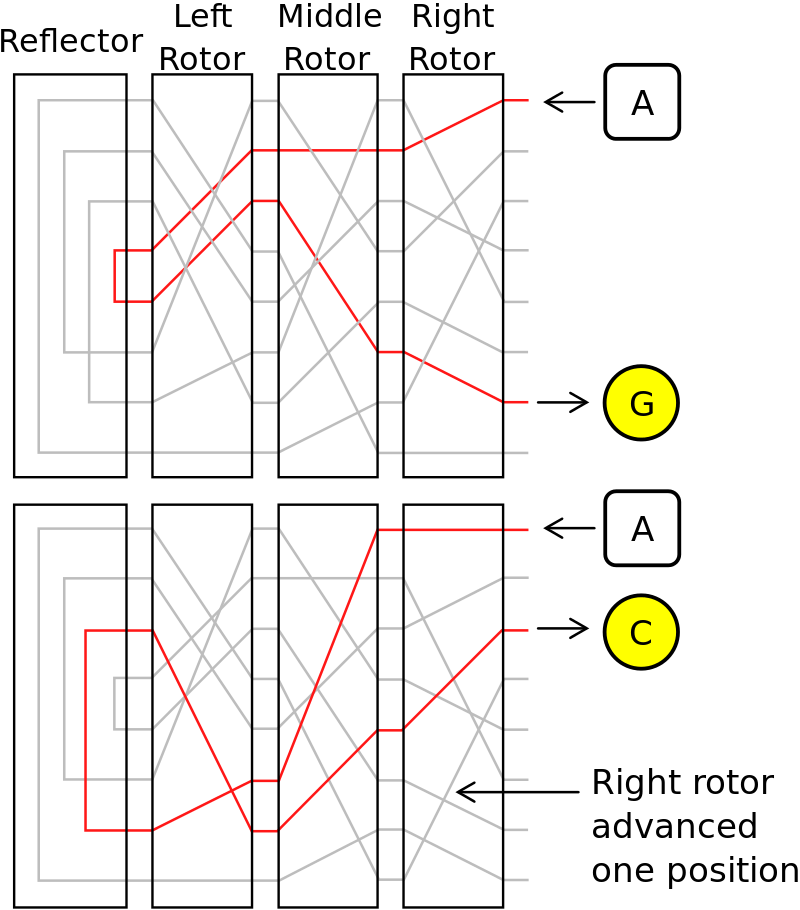
多转子编码

一个n转子的结构，密码表数量就会是$26^n$个，当n=3时，密码表数目就会达到17576，这在没有计算机的二战时期已经是一个很大的数字了，纯暴力解法需要耗费大量的人力、物力。

三转子结构

然而，严谨的德国人当然不会满足于此，谁会知道盟军会不会真的叫来17576个人来对密文进行解码呢？
接下来的地方才是恩格玛机真正变态的设计……

如果说17576个密码表仍然有纯暴力破解的可能性，只需要每个人拿一张密码表进行翻译，17576个人中一定有一个人的译文是正确的，那么如果密码表不固定的话，怎么办？
假设一个三转子结构的位置状态为AAA，即每一个转子的偏移都为0，这时候字母x传入结构会经过以下的过程

$x\stackrel{A}{\longrightarrow}x\stackrel{A}{\longrightarrow}x\stackrel{A}{\longrightarrow}x$

由于每个转子偏移都为0，所以会输出原始字符x。
如果这是张传统的密码表，即AAA的偏移状态，那么一个句子就会输出为原始的句子，这毫无疑问。

但是如果在x被编码后，就换一张密码表呢？也就是说每编码一个字母，转子状态就发生变化。这就无法用一张固定的密码表来解码一个句子了。
而恩格玛机就是这样做的，在每编码一个字母后，转子会发生一次转动，低位转子偏移量+1，对于AAA来说就会变成BAA。
对于一个句子’aaa’来说，在传统密码表AAA下的编码还是它本身aaa。但是在恩格玛机的结构下，就会经历以下的编码过程：

首先，第一个字母a进入恩格玛机，在状态为AAA的转子下编码为a；
之后，转子会转动一次，状态变为BAA，相当于换了一张密码表；
接着第二个字母a进入状态位BAA的恩格玛机

$a\stackrel{B}{\longrightarrow}b\stackrel{A}{\longrightarrow}b\stackrel{A}{\longrightarrow}b$

之后转子再次进行转动，状态变为CAA，又换了一张密码表；
最后一个字母a再次进入状态位CAA的机器

$a\stackrel{C}{\longrightarrow}c\stackrel{A}{\longrightarrow}c\stackrel{A}{\longrightarrow}c$

在密文长度不定和初始状态不确定的情况下，一个恩格玛机的结束状态是充满随机性的。当然盟军仍然可以叫来17576个人对一份密文进行破解，但是这样的工作量就会大大地提升，因为每个人在每映射玩一个字母就需要换一张字母表。而事实情况是，盟军根本叫不齐17576个人来进行这项工作。而且每天德军就会更换一次初始状态AAA，也就是说每一天盟军都需要在24小时里破解得到哪个初始的状态，否则这一天的工作就会全部白费。

由于恩格玛机的“自反特性”，恩格玛机的解密过程只需要设置相同的初始状态，即用于交流的秘钥AAA，再将密文输入恩格玛机，转子就会进行相同的转动过程对应起每一个字母的映射。

消除统计特征

尽管暴力求解不太可能实现，但是统计是可以解决很多看似困难的问题的。由于单词构造的习惯，在整个英文语料库中，字母使用的频率是不同的。比如凯撒密码，在单个字母表的映射下，每个字母的出现频率不会发生变化，只需要统计大量的密文将频率关系和日常语料库的字母频率对应起来就可以进行破解。统计特征在一张字母表下不会消除，但是如果使用两张字母表交替编码，这样的统计特征就会削弱，随着密码表数目的增加，统计直方图会趋于平稳。而恩格玛机，例如三转子恩格玛机就是使用了17576张字母表进行得编码，统计特征已经得到了十分强的削弱。

统计特征

尽管如此，统计特征却无法保证完全的消除，德国人做贼心虚，在之前的恩格玛机器基础上又加入了接线板装置。

恩格玛机器结构

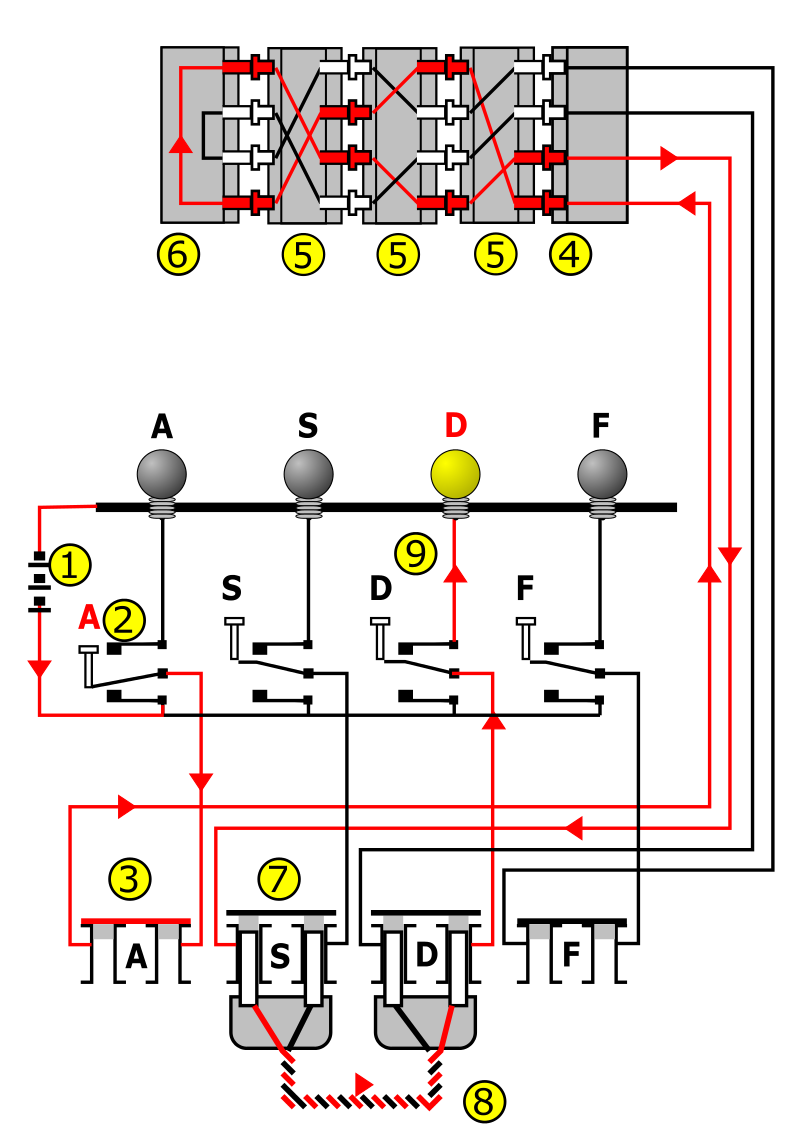
接线板的作用就是让输入的字母不直接通过转子，而是先通过装置最底层的一个通路转换成另一个字母再通过装置进行编码。接线的位置可以任意人为随机的调整，几乎完全消除了统计特征。但是德国人并没有就此满足，他们仍然担心盟军会从大量的情报密文中找出规律，因此又设计了一种二次加密方法。这种方法让每一份电报文件拥有其独特的加密秘钥，由发报者自行随机的输入，并将该秘钥放在文件头部用以另一端进行解密，一份密文可能是以下的形式。

KEY
asd asdd asd a
asd 
qwe
qw 
dq
d f...

但是这样秘钥不就毫无裸露的交给了盟军了吗？这时候再使用每天的公共秘钥对KEY进行编码，实际上德军进行了两次编码，所以一份密文实际上会是以下的形式。

YAMQAL
asd asdd asd a
asd 
qwe
qw 
dq
d f...

这样一来，“统计”这个词就失效了，因为能够利用的样本不再是报文本身，而只剩下开头的6个字母，样本不充分大就无法得到统计特征。
至此，纳粹认为他们的机器已经无法击破，然而正是这最后一步给图灵等人破解恩格玛机提供了契机……
破解恩格玛机
破解的过程可以通过上面这位UP主的视频了解。

恩格玛机的复现代码已经放到了我的github仓库Enigma-Machine。